程序化游戏地图生成浅析（一）

使用 程序化内容生成（PCG） 的优势：

• 无限地图内容：两个维度，一是单次游玩的地图内容趋近于无限，即无限大世界；二是可以生成近似无限多的世界，提升游戏的可重复游玩性；
• 节省开发成本：开发者只需要定义生成规则来描述世界最底层的机制，而不需要从上到下事无巨细地完成玩家可游玩的全部内容；
• 挑战与变化：使用程序生成地图可以很好地控制随机性，给玩家创造挑战的机会，更具趣味性；
• 动态难度调整：使用规则描述世界生成可以站在更高的维度去调控世界资源，更好地平衡游戏难度或创造特殊难度的世界。

在大多数情况下，程序化生成地图的游戏也并不能完全地摆脱传统的手工制作的部分，即便是程序化内容生成主导的世界中，也存在细粒度的部分需要开发者进行人工设计（如 Minecraft 中的村庄等内容），这同样也可以使用更细致的生成规则来描述。

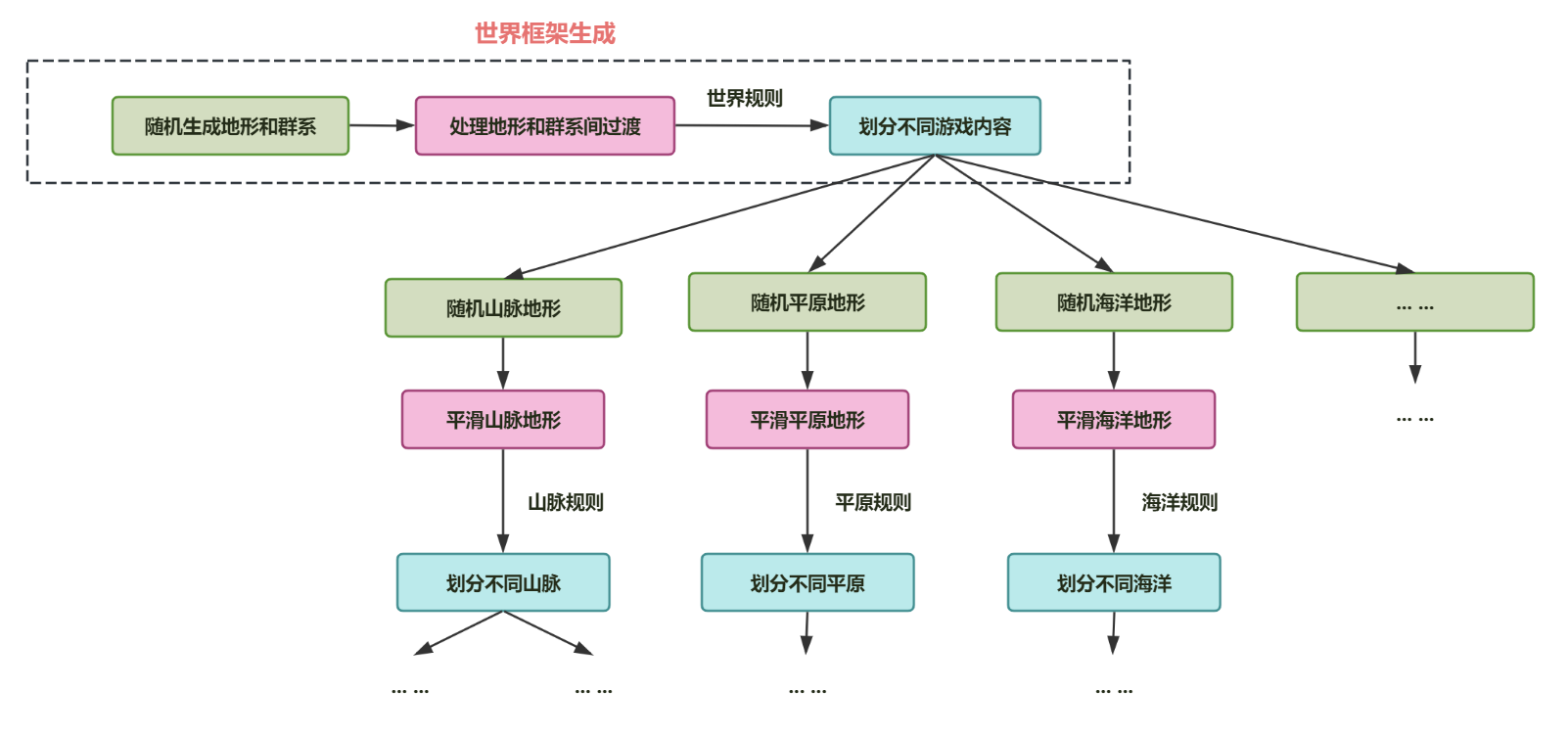
生成思路总览

对于程序化生成的游戏世界地图，可以使用分批次地、递归地类似分形的思想逐步进行细化处理，每一层处理都基本满足以下三个步骤：

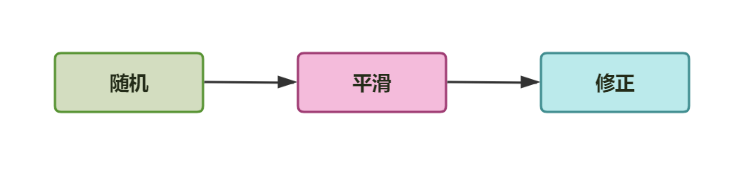
1. 随机：根据随机数或噪声算法生成最粗略的数据模板；
2. 平滑：根据当前生成内容的维度和粒度对得到的数据进行插值和过渡处理；
3. 修正：根据游戏内容和更上层的设计规则调整平滑后的世界。

一个使用此思想实现的流程可以如下所示：

在前两个步骤中，我们需要确保使用的算法满足下列三个条件：

1. 随机性：这个过程是随机的，或者说在相当大范围内不会出现重复的生成周期；
2. 可哈希：使用相同的随机数输入（种子），得到的随机内容是一致的；
3. 连续性：无论粒度大小，生成的内容都是连续且平滑的。

可哈希的特性给游戏的增量存档提供了可能，存储游戏世界信息的存档不需要在初始化生成时便保存全部数据内容，而是可以随着游戏进行，只增量存储玩家探索过或修改过的内容。

下面我们将分类讨论在随机和平滑的过程中使用的算法思路。

直接使用随机数

直接使用rand()等随机函数会存在以下问题：

• 不连续性：随机数的生成是跳跃的，直接使用时无法起到平滑的效果；
• 易受影响：虽然我们可以使用srand()等函数设置随机数的种子来确保随机数的哈希性，但是程序的其他部分可能需要使用时间来初始化随机数种子来获取更灵活的随机数，这就导致在全局环境下生成的随机数不稳定。

使用如下代码生成的灰度图，可以很清楚地看出其不连续性：

#include <graphics.h>

int main()
{
    const int width = 1280;
    const int height = 720;

    initgraph(width, height, EW_SHOWCONSOLE);

    for (int x = 0; x < width; x++)
    {
        for (int y = 0; y < height; y++)
        {
            int val = rand() % 255;
            putpixel(x, y, RGB(val, val, val));
        }
    }

    system("pause");

    return 0;
}

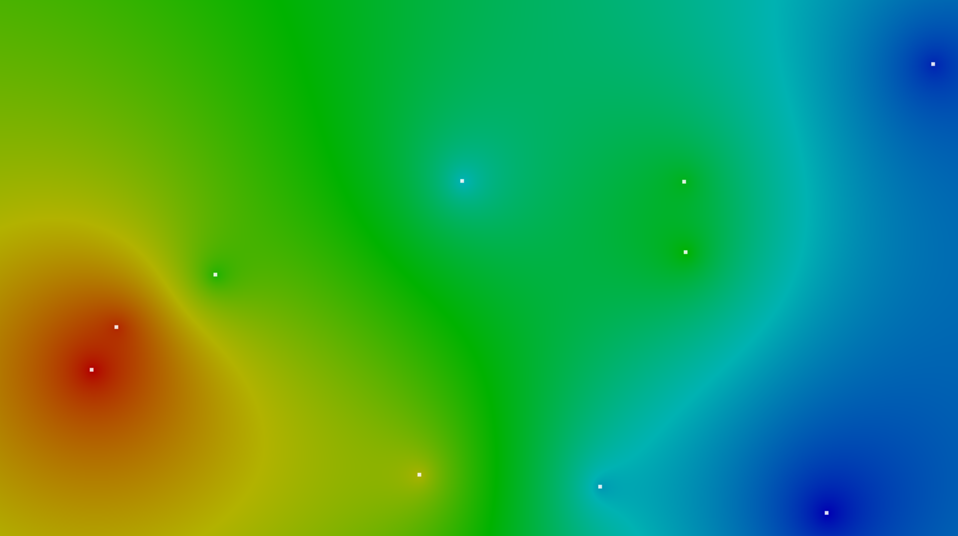
但是，这并不意味着随机数函数是无用的，我们可以直接使用随机数生成离散的影响点，再根据距离权重进行平滑处理，如《文明6》等游戏中使用的米切尔候选算法（Mitchell’s best-candidate algorithm），在处理初期时可以直接使用随机数进行候选节点的生成的，这将在后续的游戏资源生成章节再进行详细讨论。

在上古项目随机地图高度图生成过程中，也是使用了简单的先随机后平滑的思路：

平滑的噪声函数

在《基于EasyX软渲染实现常见故障艺术》一文中，提供了一种可行的随机噪声函数：

// 获取随机噪声
virtual double GetRandomNoise(double x, double y)
{
	double val = sin(x * 12.9898 + y * 78.233) * 43758.5453;
	return val - floor(val);
}

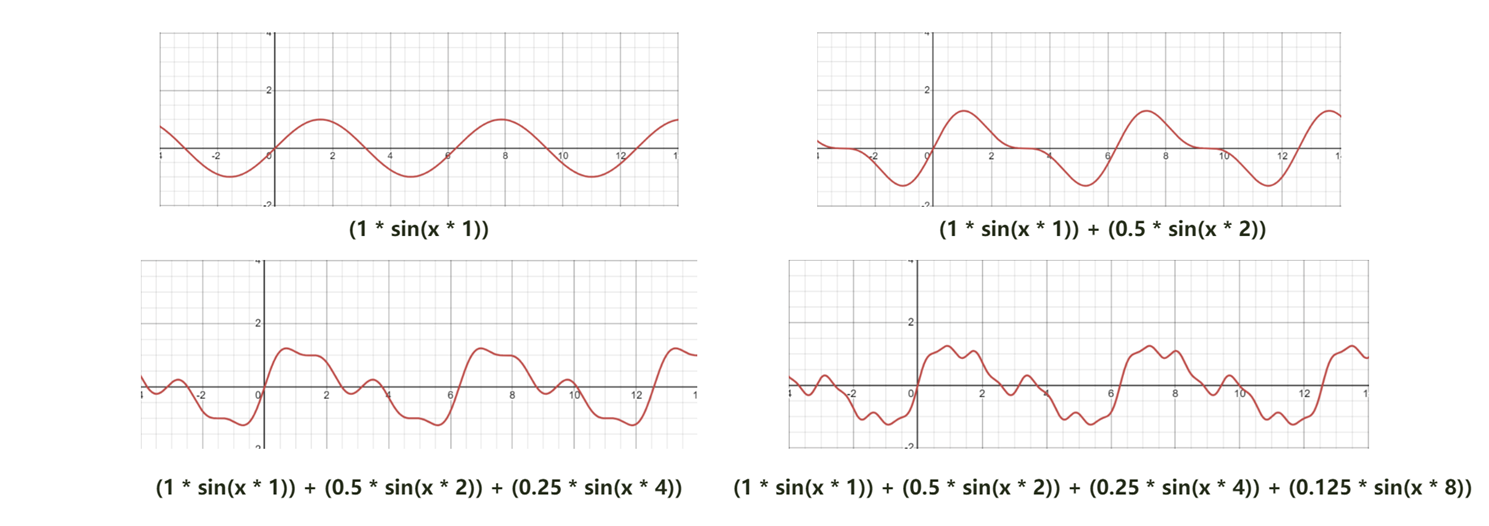
简单地，我们也可以使用正弦波叠加的思想处理类似的噪声生成：

但是，我们可以很清晰地看出，这种直接使用函数生成的噪声即便可以满足哈希性和连续性，但它们的周期性太强，直接将生成得到的计算结果应用于游戏中会导致整个世界出现大量重复地形，并不能完全满足随机性的要求：

double noise(int x, int y)
{
    double val_x = abs((1 * sin(x * 1)) + (0.5 * sin(x * 2)) + (0.25 * sin(x * 4)) + (0.125 * sin(x * 8)));
    double val_y = abs((1 * sin(y * 1)) + (0.5 * sin(y * 2)) + (0.25 * sin(y * 4)) + (0.125 * sin(y * 8)));

    // 对得到的结果进行归一化
    return (val_x + val_y) / ((1 + 0.5 + 0.25 + 0.125) * 2);
}

int main()
{
    const int width = 1280;
    const int height = 720;

    initgraph(width, height, EW_SHOWCONSOLE);

    for (int x = 0; x < width; x++)
    {
        for (int y = 0; y < height; y++)
        {
            int val = (int)(noise(x / 10, y / 10) * 255);
            putpixel(x, y, RGB(val, val, val));
        }
    }

    system("pause");

    return 0;
}

即便如此，这些生成噪声的方式，同样可以作为分形噪声等更进阶的噪声生成时的原始数据。

更进阶的噪声生成

有许多已经被实践证明满足上述需求的噪声算法，如：Perlin噪声，Simplex噪声，Wavelet噪声，Value噪声和Worley噪声等，下面将以大名鼎鼎的柏林噪声（Perlin）为例讲解实现思路。

柏林噪声本质上可以算是一种非典型的晶格噪声技术，晶格噪声是一种在离散的、规则的网格上生成的噪声，所以晶格噪声通常在规则的格点上有着明确定义的数值，而柏林噪声的特殊之处在于，在使用晶格为单位生成基础噪声后，又通过插值和平滑处理，产生了空间中连续的噪声变化。

柏林噪声的生成可以归纳为三步：

1. 梯度生成：在空间中随机生成梯度向量网格，梯度向量由每个整数坐标点（晶格）上随机确定的。这些梯度向量定义了一个在整个空间内变化的方向；
2. 插值：当需要计算某一点的噪声值时，首先确定其所处的网格单元，然后计算该点到网格单元内各个梯度向量的距离，并将这些距离用于权重插值，在这个过程中噪声得到了平滑的处理；
3. 分形：对生成得到的结果进行不同尺度的缩放和叠加，来生成更具随机性且不同粒度的结果。

#include <cmath>
#include <graphics.h>

// 生成基础噪声值
double noise(int x, int y)
{
    return fmod(sin(x * 12.9898 + y * 78.233) * 43758.5453, 1.0);
}

// 生成平滑噪声值
double smooth_noise(int x, int y) 
{
    // 计算角落、边和中心的平均噪声值
    double corners = (noise(x - 1, y - 1) + noise(x + 1, y - 1) + noise(x - 1, y + 1) + noise(x + 1, y + 1)) / 16;
    double sides = (noise(x - 1, y) + noise(x + 1, y) + noise(x, y - 1) + noise(x, y + 1)) / 8;
    double center = noise(x, y) / 4;
    // 返回平滑噪声值
    return corners + sides + center; 
}

// 线性插值
double interpolate(double a, double b, double x) 
{
    // 计算插值权重
    double ft = x * 3.1415927; 
    double f = (1 - cos(ft)) * 0.5;
    // 返回插值结果
    return a * (1 - f) + b * f; 
}

// 插值计算
double interpolated_noise(double x, double y) 
{
    // 提取整数部分和小数部分
    int integer_X = static_cast<int>(x);
    double fractional_X = x - integer_X;

    int integer_Y = static_cast<int>(y);
    double fractional_Y = y - integer_Y;

    // 计算插值点的噪声值
    double v1 = smooth_noise(integer_X, integer_Y);
    double v2 = smooth_noise(integer_X + 1, integer_Y);
    double v3 = smooth_noise(integer_X, integer_Y + 1);
    double v4 = smooth_noise(integer_X + 1, integer_Y + 1);

    double i1 = interpolate(v1, v2, fractional_X);
    double i2 = interpolate(v3, v4, fractional_X);

    // 返回插值后的噪声值
    return interpolate(i1, i2, fractional_Y); 
}

int main() 
{
    const int width = 1280;
    const int height = 720;

    initgraph(width, height);

    // 循环生成每个像素点的噪声值并转换为灰度颜色
    for (int y = 0; y < height; y++) 
    {
        for (int x = 0; x < width; x++) 
        {
            // 生成插值噪声，并控制噪声的规模
            double value = interpolated_noise(x / 50.0, y / 50.0); 
            // 将噪声值转换为灰度颜色
            COLORREF color = RGB((int)(value * 255),
                (int)(value * 255), (int)(value * 255)); 
            // 在指定位置绘制像素
            putpixel(x, y, color); 
        }
    }

    system("pause");

    return 0;
}

>>> 在 Voidmatrix’s Blog 上查看本文章 <<<