PBR 理论

欢迎大家关注原文作者 hsz！原文地址：https://www.hszsoft.com/2024/04/30/pbr-theory/

简介

PBR(Physically Based Rendering)，基于物理的渲染，指的是一些基于现实的物理原理所构成的渲染技术的集合，而非单一的某一种光照算法。

本文主要依据 LearnOpenGL 上的 PBR 理论篇，但在其中文版文章中有一些翻译问题，并且在理解上有一定难度，博主在这里对其进行了一定的简化。

为什么需要 PBR

我们为什么需要 PBR？回想我一下们在 Phone 算法中的材质：

struct Material {
    vec3 ambient;
    vec3 diffuse;
    vec3 specular;    
    float shininess;
}; 

LearnOpenGL 的作者给出了一些 特定的数据 让你调整出想要的材质的感觉。这四个参数非常不直观，它们为什么是这些值？

我们需要一套新的 描述材质 参数，它的含义应该符合人的直觉，诸如 粗糙度、金属度 这样的参数。这些参数望文生义，我们很容易就能想象出来随着它的变化，材质应该会变成什么样。

粗糙度慢慢变大的话，它会表现的像下面这个样子：

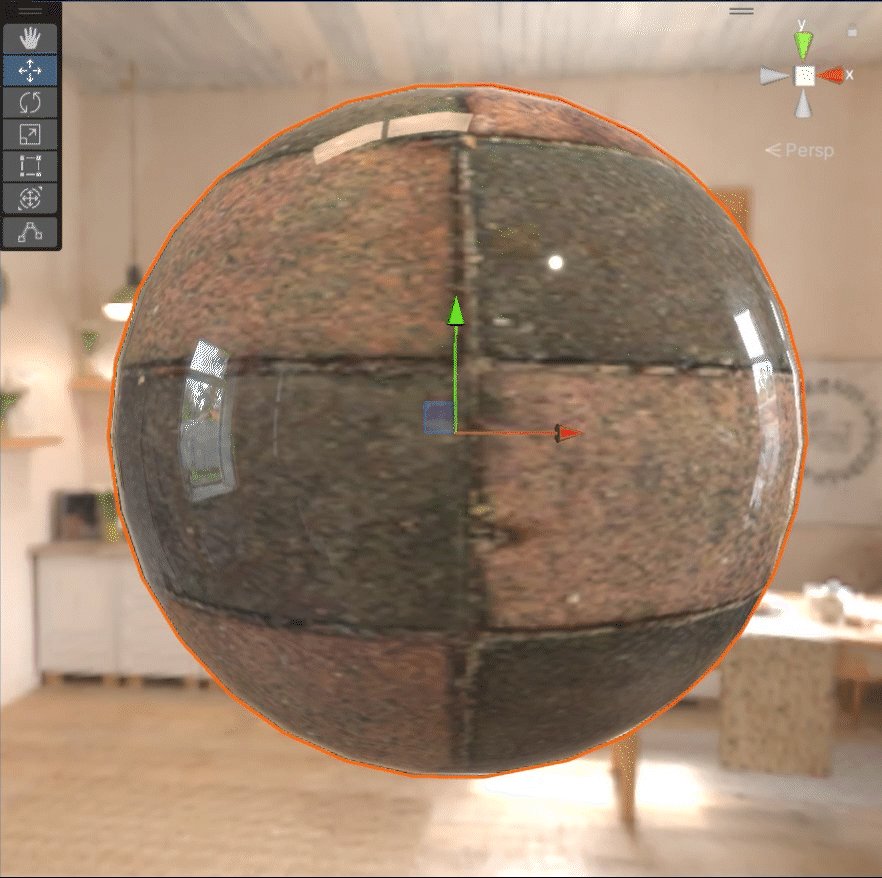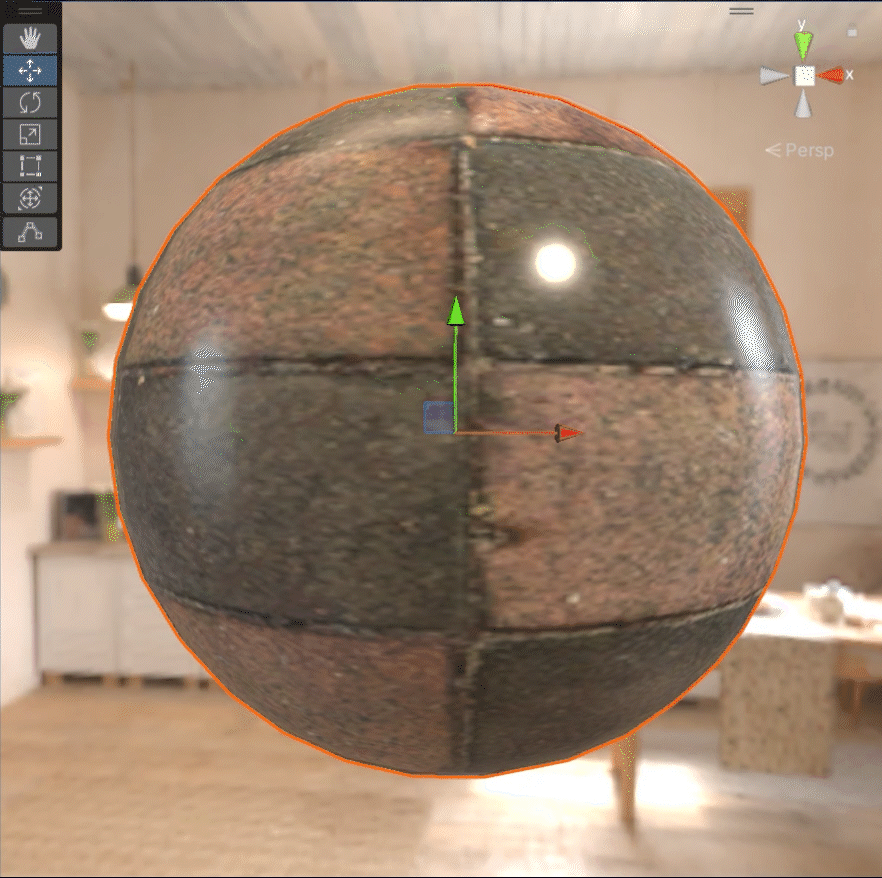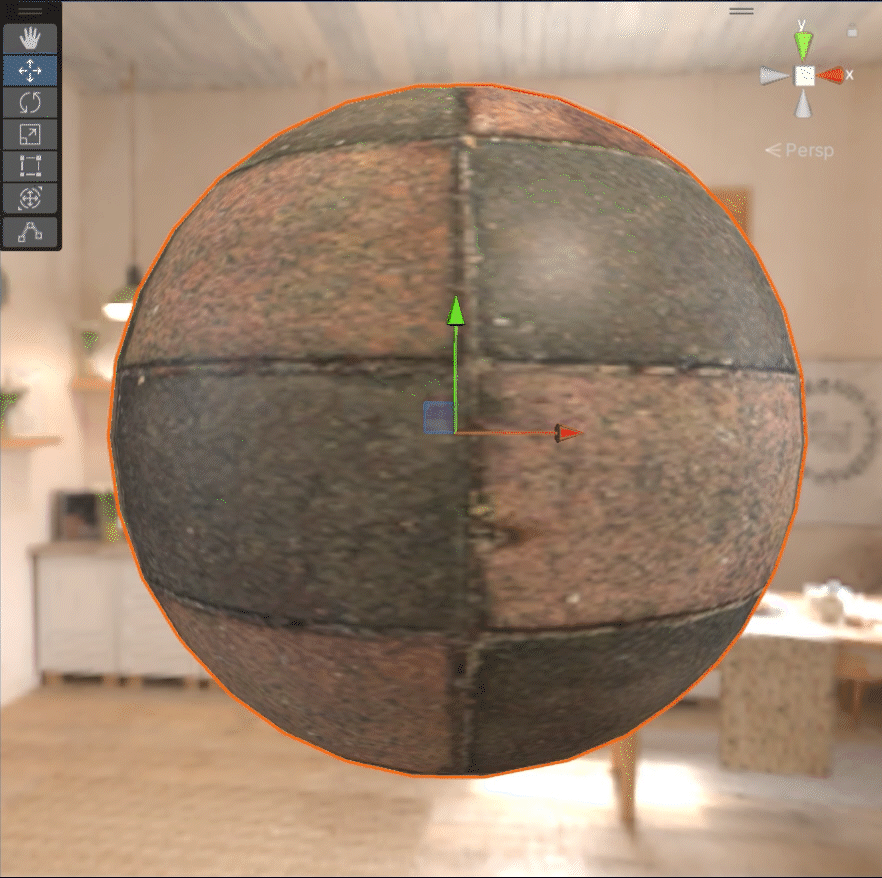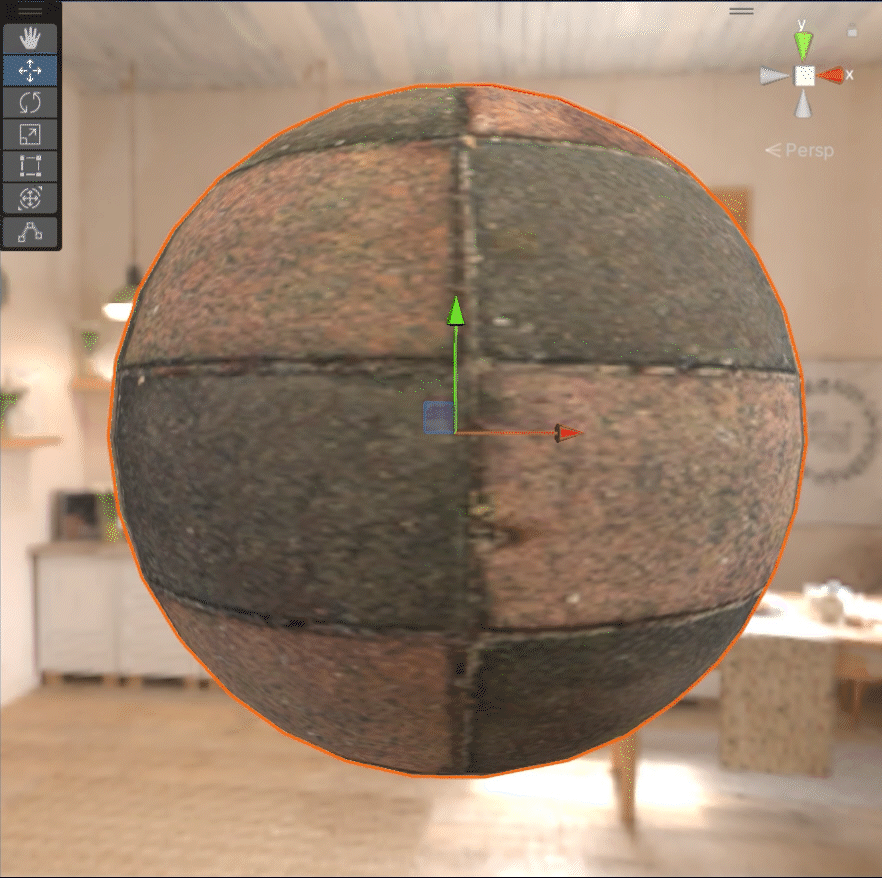
金属度慢慢变大的话，它会表现的像下面这个样子：

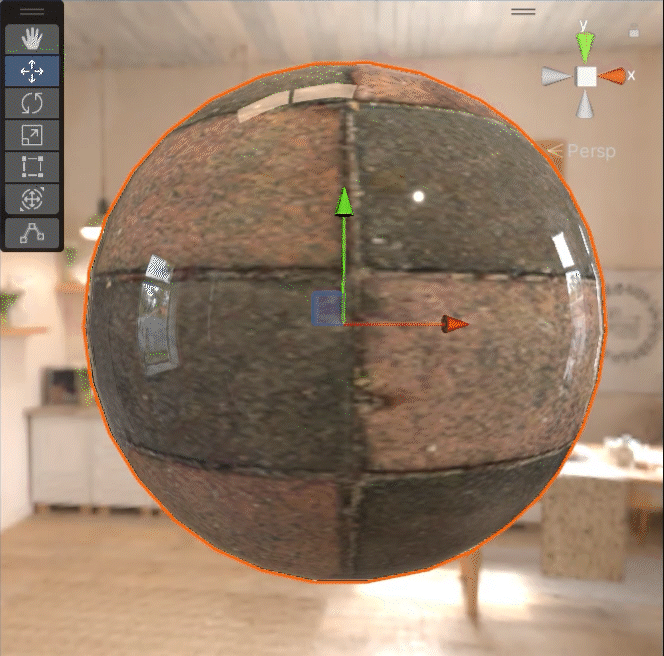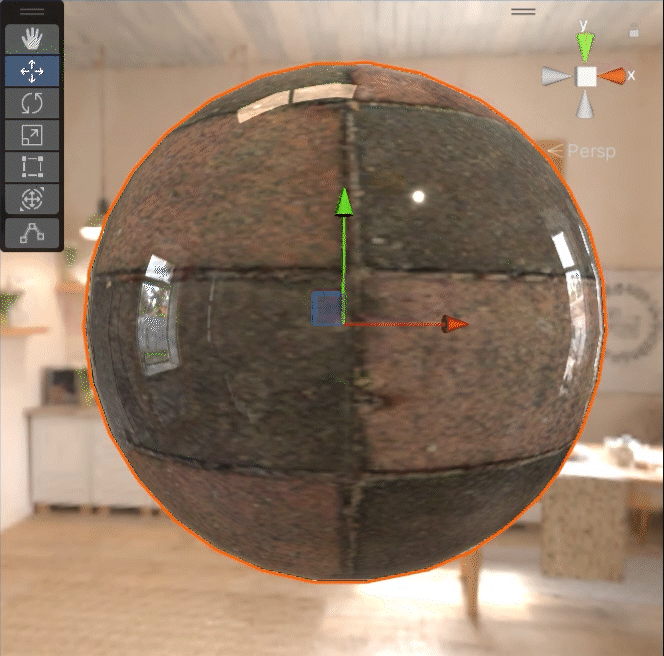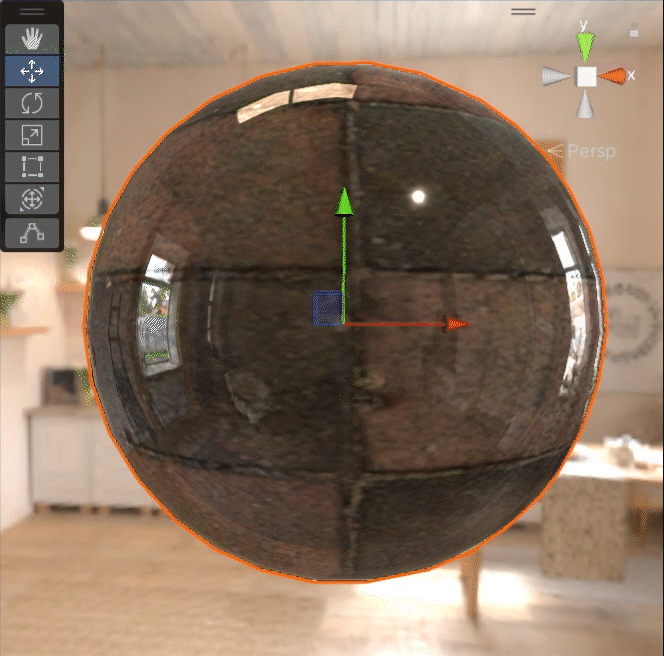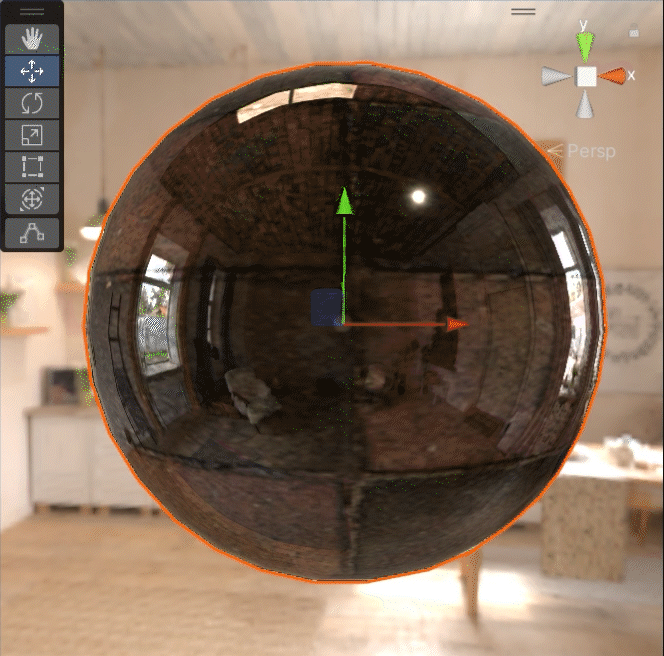
就粗糙度的变化而言的话，我们已经可以想象出来，粗糙度越大，specular 和 shininess 都会相应地减小，diffuse 也会有相应的变化。那么，这里应该有一些处理 diffuse 和 specular 随着粗糙度的值的变化而变化的公式。这些公式的是怎么来的？

基于 物理而来，我之所以要强调这个词，是因为现代计算机的算力有限，我们无法完全按照现实生活的物理公式来计算的。我们要讨论的算法得到的都是一些近似结果，但它们有着非常高的效率。

PBR 理论

前面提到过 PBR 并非一种单一的光照算法，根据其实现的不同，它有很多种 工作流（在输入参数上有区别），比较常用的有金属/粗糙度(Metal/Roughness)工作流和镜面反射/光泽度(Specular/Glossiness)工作流。

不管如何，它们都要满足下面这些条件：

• 基于微平面的表面模型
• 能量守恒
• 应用基于物理的双向反射分布函数

博主的这篇文章会对金属/粗糙度(Metal/Roughness)工作流进行讲解。

微平面理论 (Microfacets Theory)

这个理论认为没有平面是完全光滑的。由于微平面微小到无法用像素级别的量级对其进行区分，因此我们可以假设一个 Roughness(粗糙度) 参数，用 统计学 的方法来估计微平面的粗糙程度。我们可以基于一个平面的粗糙度来计算出众多微平面中，朝向方向沿着 半程向量 方向的比例。

粗糙度介于 0 到 1，刚才我们看到的变化类似于这样：

能量守恒 (Energy Conservation)

出射光线的能量永远不能超过入射光线的能量（发光面除外）。随着粗糙度的上升，镜面反射区域会变大，反射亮度会下降。如果每个像素的镜面反射强度都一样，就违背了这个定律。这也是刚才我们看到的光滑平面的反射更强烈而粗糙平面的反射更昏暗的原因。

当一束光碰到一个表面时，会分离成 反射 部分和 折射 部分。反射部分就是我们常说的镜面(Specular)光照，而折射部分就是我们所说的漫反射(Diffuse)光照。为什么折射部分是漫反射光照呢？因为我们这里做了个假设，折射光进入物体后的情况会很复杂，它会像这样：

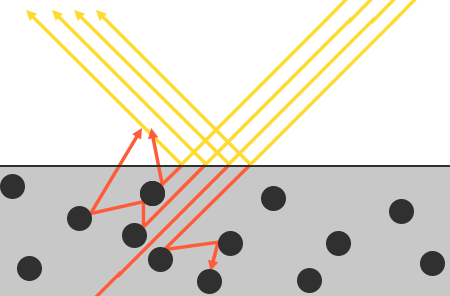
我们只考虑在物体的表面附近反射出来的，它们也就构成了漫反射光。对于那些深入了物体表面的部分，我们假设它们全部被吸收。现实的情况是确实有一部分光可能会在比较远的比方再次反射出来，一些被称为 次表面散射(Subsurface Scattering)技术 的着色器技术将这个问题考虑了进去，它们显著地提升了一些诸如皮肤，大理石或者蜡质这样材质的视觉效果，不过伴随而来的代价是性能的下降。

那我们不难想出，反射和折射二者是 互斥 的关系，所以一般会有以下的计算：

float kS = calculateSpecularComponent(...); // 反射/镜面部分
float kD = 1.0 - ks;                        // 折射/漫反射部分

不过，对于 金属 表面，所有的折射光都会被直接吸收而不会散开，只留下镜面反射光。金属度越高的表面，其原本的颜色越少，周围环境的颜色越多，所以会增加一点东西：

float kS = calculateSpecularComponent(...);
float3 k_d = (1.0 - k_s) * (1.0 - metallic);

说了这么多，接下来就可以看看这两个理论是如何被应用的了。

双向反射分布函数 (BRDF)

这个名字看着非常高上大，并且是 PBR 的核心，让我们来慢慢理解。

首先，BRDF 是一个函数，它接受 入射光方向向量、出射光方向向量 作为输入，所以是 双向，实际上还有法向量 n，不过在公式中我们一般认为它是已知的。然后，它接受我们刚才说的 粗糙度 和 金属度 之类的参数，最后返回这束光线对这个片段贡献的 RGB 颜色。在使用中，我们在片段着色器中遍历会影响到这个片段的灯光，并且将其值累加起来。

不过法向量 n 的计算实际上还是比较麻烦的，它需要计算切线空间，详细内容可以看 LearnOpenGL 中的 法线贴图。

不难发现，其实 Phone 模型就是一个 BRDF，不过问题在于它并不遵循物理规则。回想一下我们在 多光源 中的代码：

void main()
{    
    // properties
    vec3 norm = normalize(Normal);
    vec3 viewDir = normalize(viewPos - FragPos);
    
    // phase 1: directional lighting
    vec3 result = CalcDirLight(dirLight, norm, viewDir);
    // phase 2: point lights
    for(int i = 0; i < NR_POINT_LIGHTS; i++)
        result += CalcPointLight(pointLights[i], norm, FragPos, viewDir);    
    // phase 3: spot light
    result += CalcSpotLight(spotLight, norm, FragPos, viewDir);    
    
    FragColor = vec4(result, 1.0);
}

这里的 CalDirLight、CalPointLight、CalSpotLight 都是 BRDF，我们之前直接通过累加来计算其贡献值，PBR 中我们计算也是靠这样进行累加。这里其实有 积分 的行为，不过现在暂时不用了解，我们会在后面的 IBL 中讲解它（反射率方程），而现在只需要知道正是因为积分，所以公式中会存在 标准化 的步骤。

现在我们需要一个遵循物理规则的 BRDF，这也有很多种实现，我们可以使用一种被称为 Cook-Torrance BRDF 的模型。Cook-Torrance BRDF 兼有漫反射和镜面反射两个部分：

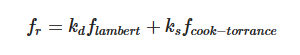
公式的左侧表示的是 lambertian 反射，用于表示漫反射的部分，用如下公式来表示：

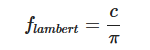
lambertian 中的 c 表示材质表面颜色，在我们的工作流中对应着 albedo 纹理，除以 π 是为了对漫反射光进行 标准化。

公式的右侧是其镜面反射的部分，它的形式如下：

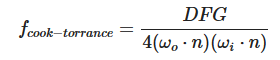
和前面一样，分母依旧是用来进行 标准化 的。这里的字母 D、F、G 分别代表法线分布函数(Normal Distribution Function)，菲涅尔方程(Fresnel Rquation)和几何函数(Geometry Function)。

• 法线分布函数：估算在受到表面粗糙度的影响下，朝向方向与半程向量一致的微平面的数量。这是用来估算微平面的主要函数。

• 几何函数：描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候，平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。

• 菲涅尔方程：菲涅尔方程描述的是在不同的观察角度下被反射的光线所占的百分比。它一般就等于 Cook-Torrance BRDF 中的那个 kd。

在我们的实现中，前两者通过 粗糙度 计算出一个 float 值，而菲涅尔方程主要通过 金属度 计算出一个类型为 vec3 的颜色值。

法线分布函数

法线分布函数从统计学上近似表示材质表面法向量与半程向量取向一致的比率。目前有很多种 NDF 都可以根据一些粗糙度参数估算微平面的总体取向度。

NDF 接受 法向量、半程向量、粗糙度 为参数，返回一个 float 值。这里我们使用 Trowbridge-Reitz GGX：

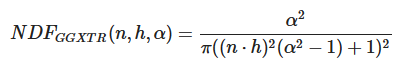
在公式中 h 表示我们的半程向量，而 α 表示表面的粗糙度。

当粗糙度很低（也就是说表面很光滑）的时候，与半程向量取向一致的微平面会高度集中在一个很小的半径范围内。由于这种集中性，NDF 最终会生成一个非常明亮的斑点。但是当表面比较粗糙的时候，微平面的取向方向会更加的随机。你将会发现与 h 向量取向一致的微平面分布在一个大得多的半径范围内，但是同时较低的集中性也会让我们的最终效果显得更加灰暗。

它的 GLSL 代码实现如下：

float D_GGX_TR(vec3 N, vec3 H, float a)
{
    float a2     = a*a;
    float NdotH  = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;

    float nom    = a2;
    float denom  = (NdotH2 * (a2 - 1.0) + 1.0);
    denom        = PI * denom * denom;

    return nom / denom;
}

几何函数

几何函数从统计学上近似的求得了微平面间相互遮蔽的比率，这种相互遮蔽会损耗光线的能量，最终导致材质表面整体显得更加灰暗。

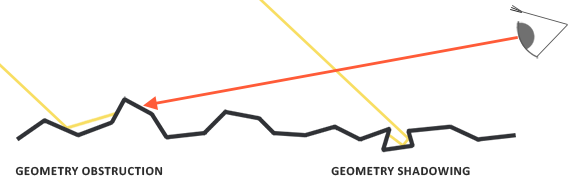
它接受 观察方向向量、光线方向向量、法向量、粗糙度 作为输入，最终返回一个 float 值。粗糙度越高的表面其微平面间相互遮蔽的概率就越高，这个 float 值就越小，这里我们使用 GGX 与 Schlick-Beckmann 近似 的结合体，即 Schlick-GGX：

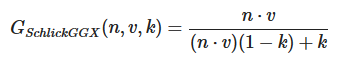
这里 k 是 α 的 重映射，取决于我们要使用的是针对直接光照还是针对 IBL 光照的几何函数，我们暂时只介绍直接光照的重映射：

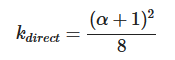
材质表面自成阴影的分布情况同时和 观察方向 与 光线方向 有关，在刚才那张微平面的图中，我们可以注意到有些光线因为我们的观察方向比较特别而形成遮挡，我们称之为 几何遮蔽(Geometry Obstruction)，有些则和我们的观察方向无关，光线入射进来的时候就已经被遮挡了，我们称之为 几何阴影(Geometry Shadowing)。为了同时考虑二者的影响，我们使用 史密斯法 来进行计算：

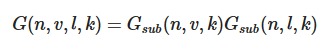
其中，Gsub 即为我们的 Schlick-GGX，如此计算，随着粗糙度的提高，材质表面的视觉效果如下：

使用 GLSL 编写的实现如下：

float GeometrySchlickGGX(float NdotV, float k)
{
    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;

    return nom / denom;
}

float GeometrySmith(vec3 N, vec3 V, vec3 L, float k)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx1 = GeometrySchlickGGX(NdotV, k);
    float ggx2 = GeometrySchlickGGX(NdotL, k);

    return ggx1 * ggx2;
}

菲涅尔方程

菲涅尔方程描述的是被反射的光线对比被折射的光线的比率，这个比率会随着我们观察角度的不同而不同。我们正是利用这个方程计算出 反射光线(fs) 的部分，并进一步得到光线剩余的能量计算出 折射光线(fd) 的部分。它会影响我们看到的 specular 部分的颜色和强度，接下来请看原理。

当垂直观察时，任何材质表面都有一个 基础反射率，但是我们的观察角度慢慢与材质表面趋近于平行时，所有反光都会变得明显起来。想象一下，如果你站在湖边低头看脚下的水，你会发现水是透明的，反射并不强烈；如果你看远处的湖面，你会发现它们的反射特别强烈。如果从理想的 90° 进行观察，理论上所有平面都能完全反射光线。这种现象体现在了菲涅尔方程里，不过它的本体过于复杂，好在我们可以用 Fresnel-Schlick 近似法求得近似解：

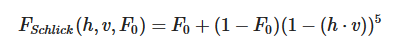
这个方程接受 F0 (color)、观察方向向量、半程向量 作为输入，最后返回一个 vec3 颜色值。其中，F0 表示垂直观察一个材质表面时的反射率，即基础反射率，它是一个颜色值，它可以通过材质的 折射率 预计算得出。经过这个方程的计算后，我们观察一个球体表面时可以注意到，我们越是朝球体边缘上看，反光越强：

那为什么 F0 是一个 color 值而不是一个 float 值呢？你可以在现实中进行观察，对于非金属表面，它的高光是灯光的颜色，但如果是金属表面的话，它的高光会带一点它本来的颜色。比如对于黄金的话，它的高光也是金色的。

那么，既然说到 F0 应该进行预计算，那么我们应该怎么算呢？对于非金属材质，我们可以使用这个公式：

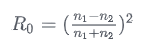
之所以可以用它来计算，是因为这里忽略掉了非金属材质的 消光系数，因为它相当小，而金属材质的消光系数是不能忽略的。

那这意味着我们要对金属和非金属使用两套不同的公式来预计算出其 F0 吗？这有点麻烦，所以让我们来观察一下不同材质的基础反射率：

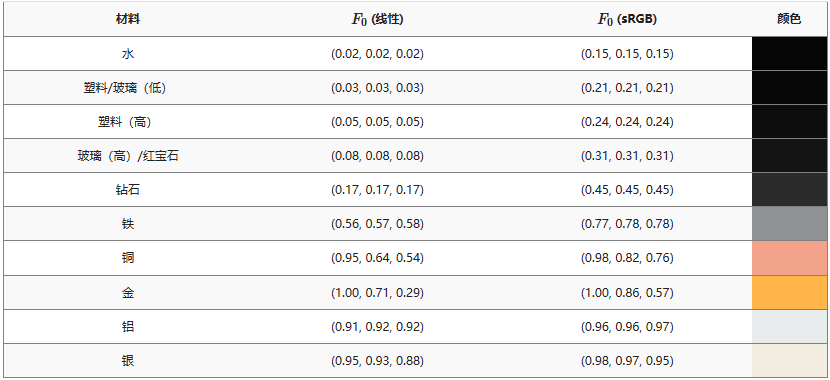
在这里可以看到，所有非金属材质表面的基础反射率都不会高于 0.17，这实际上是例外情况而非普遍情况，对于它们，我们可以用 (0.04, 0.04, 0.04) 就可以得到足够好的结果了。然后，对于金属材质，我们需要添加一点其表面的纹理颜色来补充，这是因为金属表面会吸收所有的折射光线而没有漫反射，我们一般是这样实现的：

vec3 F0 = vec3(0.04);
F0      = mix(F0, surfaceColor.rgb, metalness);

这里引入了一个新的值，即 金属度(metalness)，用于描述一个材质表面是金属还是非金属的，也就是，它的 specular 是否带有原本材质的颜色。

理论上来说，一个表面的金属度应该是二元的：要么是金属要么不是金属，不能两者皆是。但是，大多数的渲染管线都允许在 0.0 至 1.0 之间线性的调配金属度。这主要是由于材质纹理精度不足以描述一个拥有诸如细沙/沙状粒子/刮痕的金属表面。通过对这些小的类非金属粒子/刮痕调整金属度值，我们可以获得非常好看的视觉效果。

最后把我们插值得到的 F0 输入到 Fresnel-Schlick 的函数中即可，它的代码实现如下：

vec3 SchlickFresnel(float HdotV, vec3 F0)
{
    float m = clamp(1 - HdotV, 0, 1);
    float m2 = m * m;
    float m5 = m2 * m2 * m; // pow(m,5)
    return F0 + (1.0 - F0) * m5;
}

PBR 工作流

在得到 BRDF 后，我们就已经可以计算 PBR 了，可以暂时不用在意 渲染方程 的存在。

在我们实际的工作流中，这些材质的参数是通过纹理输入进来的，使用纹理我们可以逐个片段的来控制每个表面上特定的点对于光线是如何相应的。

下面是一个比较经典的 PBR 渲染管线的纹理列表，还有它最终的视觉输出：

其中，从左到右：

• 反照率(Albedo)：指定材质的 表面颜色 或 基础反射率，这和我们之前使用的漫反射纹理很像，但漫反射的图像中常常包含一些细小的阴影和裂纹，而在 PBR 中这些东西会保存在别的纹理中。

• 法线(Normal)：详见 LearnOpenGL 的 法线贴图，它可以逐片段指定独特的法线制造出起伏不平的假象，在模型的定点数较低的情况下丰富细节。

• 金属度(Metallic)：指定该纹素是否是金属质地的，根据引擎设置的不同，美术师可以将其编写为灰度值或1、0这样的二元值。

• 粗糙度(Roughness)：指定某一个纹素有多粗糙，有些引擎采用的是 光滑度(Smoothness) 贴图，在采样时用 (1.0 - smoothness) 后就可以转换为粗糙度了。

• 环境光遮罩(Ambient Occlusion)：指定了一个额外的阴影因子，反照率纹理上砖块的裂缝部分没有任何阴影信息，而 AO 贴图就会把它们指定出来。

这个 AO 并没有在前面提到过，在实现中，它并不在 BRDF 的计算中进行，目前直接光照的值都会累加在 Lo 中，而最后的颜色值是这样计算的：

vec3 ambient = vec3(0.03) * albedo * ao;
vec3 color = ambient + Lo;

这里我们暂时使用 0.03 来表示环境光的强度，而想要得到更好的视觉效果，就需要看之后说到的 IBL 了。

PBR 应用代码

刚才在介绍 BRDF 时博主贴出了 Phone 模型的代码，那么接下来我们来看看 PBR 的片段着色器中代码是什么样子的，接下来，我们假设场景中有四个灯光：

vec3 ReflectanceEquation(vec3 N, vec3 V, vec3 L, vec3 albedo, vec3 radiance, float roughness, float metallic)
{
    roughness = max(roughness, 0.05);

    vec3 H = normalize(L + V);
    float NdotL = max(dot(N, L), 0);
    float NdotV = max(dot(N, V), 0);
    float NdotH = max(dot(N, H), 0);
    float HdotV = max(dot(H, V), 0);

    float F0 = mix(vec3(0.04), albedo, metallic);

    float D = DistributionGGX(NdotH, roughness);
    float F = FresnelSchlick(NdotV, F0);
    float G = GeometrySmith(NdotV, NdotL, roughness);

    vec3 k_s = F;
    vec3 k_d = (vec3(1.0) - k_s) * (1.0 - metallic);
    
    vec3 f_diffuse = albedo / PI;
    vec3 f_specular = (D * F * G) / (4.0 * NdotV * NdotL + 0.0001);

    return (k_d * f_diffuse + f_specular) * radiance * NdotL;
}
// ----------------------------------------------------------------------------
void main()
{		
    vec3 albedo     = pow(texture(albedoMap, TexCoords).rgb, vec3(2.2));
    float metallic  = texture(metallicMap, TexCoords).r;
    float roughness = texture(roughnessMap, TexCoords).r;
    float ao        = texture(aoMap, TexCoords).r;

    vec3 N = GetNormalFromMap();
    vec3 V = normalize(camPos - WorldPos);

    // calculate reflectance at normal incidence; if dia-electric (like plastic) use F0 
    // of 0.04 and if it's a metal, use the albedo color as F0 (metallic workflow)    
    vec3 F0 = vec3(0.04); 
    F0 = mix(F0, albedo, metallic);

    // reflectance equation
    vec3 Lo = vec3(0.0);
    for(int i = 0; i < 4; ++i) 
    {
        vec3 radiance = lightColors[i];
        vec3 L = normalize(lightPositions[i] - WorldPos);

        // calculate per-light attenuation
        float distance = length(lightPositions[i] - WorldPos);
        float attenuation = 1.0 / (distance * distance);

        Lo += ReflectanceEquation(N, V, L, albedo, radiance, roughness, metallic) * attenuation;
    }   
    
    // ambient lighting (note that the next IBL tutorial will replace 
    // this ambient lighting with environment lighting).
    vec3 ambient = vec3(0.03) * albedo * ao;
    
    vec3 color = ambient + Lo;

    // HDR tonemapping
    color = color / (color + vec3(1.0));
    // gamma correct
    color = pow(color, vec3(1.0/2.2)); 

    FragColor = vec4(color, 1.0);
}

这份代码中我们在场景中添加了四个点光源，并且根据距离计算了它的衰减。

把反射率方程 ReflectanceEquation 封装好之后，这份代码实际上和 Phone 看起来就会比较像了，不过需要注意一下结尾的把结果映射到 HDR 和 伽马矫正 的步骤，在这里不做过多赘述。

结语

其实可以看到，PBR 最重要的东西便在于它的这个 BRDF，我们除了可以使用 Metallic-Roughness 来描述材质以外，行业内比较主流的方案还有 Specular-Glossiness 材质，这两种方案各有优缺点。实际上，只要愿意，我们可以用各种各样的参数去定义一个材质的属性，不过，迪士尼曾就这件事提出了它们自己的原则，即 Disney Principled BRDF，内容如下：

• 应使用直观的参数，而不是物理类的晦涩参数（更符合艺术家的直觉）
• 参数应尽可能少
• 参数在其合理范围内应该为 0 到 1
• 允许参数在有意义时超出正常的合理范围
• 所有参数组合应尽可能健壮和合理

以这些理念为基础，迪士尼动画工作室对每个参数的添加进行了把关，最终得到了一个颜色参数 (baseColor) 和下面描述的十个标量参数：

• baseColor（固有色）：表面颜色，通常由纹理贴图提供。
• subsurface（次表面）：使用次表面近似控制漫反射形状。
• metallic（金属度）：金属（0 = 电介质，1 =金属）。这是两种不同模型之间的线性混合。金属模型没有漫反射成分，并且还具有等于基础色的着色入射镜面反射。
• specular（镜面反射强度）：入射镜面反射量。用于取代折射率。
• specularTint（镜面反射颜色）：对美术控制的让步，用于对基础色（basecolor）的入射镜面反射进行颜色控制。掠射镜面反射仍然是非彩色的。
• roughness（粗糙度）：表面粗糙度，控制漫反射和镜面反射。
• anisotropic（各向异性强度）：各向异性程度。用于控制镜面反射高光的纵横比。（0 =各向同性，1 =最大各向异性。）
• sheen（光泽度）：一种额外的掠射分量（grazing component），主要用于布料。
• sheenTint（光泽颜色）：对sheen（光泽度）的颜色控制。
• clearcoat（清漆强度）：有特殊用途的第二个镜面波瓣（specular lobe）。
• clearcoatGloss（清漆光泽度）：控制透明涂层光泽度，0 = “缎面（satin）”外观，1 = “光泽（gloss）”外观。

引用文章

LearnOpenGL PBR 理论
https://learnopengl-cn.github.io/07%20PBR/01%20Theory/

LearnOpenGL PBR 光照
https://learnopengl-cn.github.io/07%20PBR/02%20Lighting/

菲涅尔方程（Fresnel Equation）
https://zhuanlan.zhihu.com/p/375746359

草履虫都能看懂的 PBR 讲解
https://zhuanlan.zhihu.com/p/137013668

几何光学下的光线传播——光的反射、折射、菲涅耳公式
https://zhuanlan.zhihu.com/p/480405520

基于物理的渲染（PBR）白皮书 | 迪士尼原则的BRDF与BSDF相关总结
https://cloud.tencent.com/developer/article/1427571